| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- Javascript #코드스테이츠
- html
- 원시자료형
- codestate
- cta버튼
- JavaScript
- condestates
- cta button
- Router
- Prototype
- OOP
- frontend
- 프로토타입
- 자바스크립트
- codestates
- 객체지향
- 개발자
- 참조자료형
- 호스트인식
- CDD
- css
- self reliance
- WAI-ARIA
- JS
- 계산기
- 프론트엔드
- css in js
- 회고
- 코드스테이츠
- 코드스테이스
- Today
- Total
jh.nrtv
[Python] 순열, 조합 , 중복순열, 중복조합 본문
모든 경우의 수를 확인하는 알고리즘인 완전탐색 구현시 자주 쓰이는 Python 라이브러리를 정리하고자 한다.
✅ 순열 permutations
반복 가능한 길이 n의 객체에 대해서
중복을 허용하지 않고
r개를 뽑아서 나열한다. (순서 유의미)
경우의 수 : nPr = nCr * r!
from itertools import permutations
# 반복문 for i in permutations({반복할 N길이 배열}, {나열할r숫자}):
# 하면 경우의 수가 () 튜플 형태로 반복됨
for i in permutations([1,2,3,4], 2):
print(i, end=" ")
# >(1, 2) (1, 3) (1, 4) (2, 1) (2, 3) (2, 4) (3, 1) (3, 2) (3, 4) (4, 1) (4, 2) (4, 3)
#혹은 아래와 같이 사용
_list = [1, 2, 3]
perm = list(permutations(_list, 2))
print(perm)
# [(1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2)]
✅ 조합 combinations
반복 가능한 길이 n인 객체에서
중복을 허용하지 않고
r개를 뽑는다. (순서 무의미)
경우의 수 : nCr
from itertools import combinations
# 반복문 for i in combinations({반복할 N길이 배열}, {뽑을r숫자}):
# 하면 경우의 수가 () 튜플 형태로 반복됨
for i in combinations([1,2,3,4] , 2):
print (i , end=" ")
# >(1, 2) (1, 3) (1, 4) (2, 3) (2, 4) (3, 4)
#혹은 아래와 같이 간단하게 씀
_list = [1, 2, 3]
combi = list(combinations(_list, 2))
print(combi)
# >>> [(1, 2), (1, 3), (2, 3)]
✅ 중복순열 product
반복 가능한 길이 n인 객체에서
중복을 허용해서
r개를 배열한다. (순서 유의미)
product 메소드는 데카르트의 곱을 나타냄 (= 각각의 리스트에서 하나씩 뽑을 조합)
- '데카르트의 곱' 이란?
두 집합 A, B가 있을 때, 이 두 집합의 데카르트 곱은 아래와 같이 정의한다.
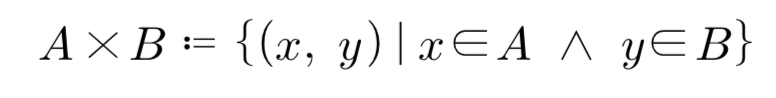
즉, A집합의 x이면서 B집합에서는 y인 순서쌍들의 집합이다. 다시 말해, 각 집합에 있는 모든 원소들은 서로 서로 모두 만난다. 또는 모든 경우의 수의 쌍이 된다고 표현할 수 있겠다. ( ) 안에 있는 것은 튜플로 순서 쌍이라고 보면 되겠다. 아래의 경우, (x, y, z) 집합과 (1, 2, 3) 집합의 데카르트 곱의 결과를 보여준다.
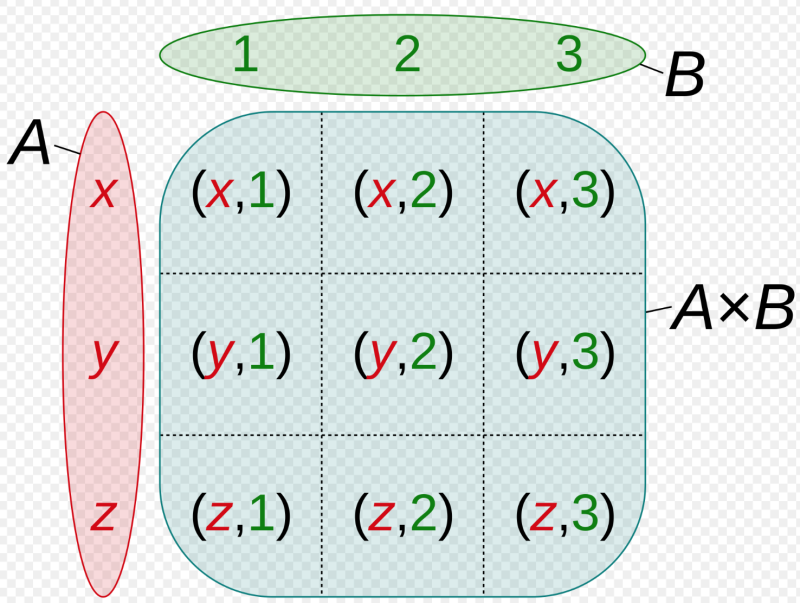
-> 이를 중복순열 구현에 활용함 ( 하나씩 뽑을 리스트를 모두 n길이의 동일한 배열로 넣으면 = 중복순열 )
from itertools import product
#사용법1
# for i in product( 뽑을 배열A, 뽑을 배열B ... )
# A에서 하나 뽑고, B에서 하나뽑고 .. 해서 r개 뽑은 경우의 수 튜플형태로 반환
for i in product([1,2,3],'ab'):
print(i, end=" ")
#>>>(1, 'a') (1, 'b') (2, 'a') (2, 'b') (3, 'a') (3, 'b')
for i in product(range(3), range(3), range(3)):
print(i, end=" ")
#>>>(0, 0, 0) (0, 0, 1) (0, 0, 2) (0, 1, 0) (0, 1, 1) (0, 1, 2) (0, 2, 0) (0, 2, 1) (0, 2, 2) (1, 0, 0) (1, 0, 1) (1, 0, 2) (1, 1, 0) (1, 1, 1) (1, 1, 2) (1, 2, 0) (1, 2, 1) (1, 2, 2) (2, 0, 0) (2, 0, 1) (2, 0, 2) (2, 1, 0) (2, 1, 1) (2, 1, 2) (2, 2, 0) (2, 2, 1) (2, 2, 2)from itertools import product
#사용법2
#for i in product( 길이n의배열, repeat=반복할숫자 ) :
#하면 i = 튜플형태의 경우의수 반복해서 나옴
for i in product([1,2,3], repeat=3):
print(i , end=" ")
# >>>(1, 1, 1) (1, 1, 2) (1, 1, 3) (1, 2, 1) (1, 2, 2) (1, 2, 3) (1, 3, 1) (1, 3, 2) (1, 3, 3) (2, 1, 1) (2, 1, 2) (2, 1, 3) (2, 2, 1) (2, 2, 2) (2, 2, 3) (2, 3, 1) (2, 3, 2) (2, 3, 3) (3, 1, 1) (3, 1, 2) (3, 1, 3) (3, 2, 1) (3, 2, 2) (3, 2, 3) (3, 3, 1) (3, 3, 2) (3, 3, 3)
#혹은 아래와 같이
arr= list(product(['A','B','C','D','E'], repeat=2)
print(arr)
#>>>[('A', 'A'), ('A', 'B'), ('A', 'C'), ('A', 'D'), ('A', 'E'), ('B', 'A'), ('B', 'B'), ('B', 'C'), ('B', 'D'), ('B', 'E'), ('C', 'A'), ('C', 'B'), ('C', 'C'), ('C', 'D'), ('C', 'E'), ('D', 'A'), ('D', 'B'), ('D', 'C'), ('D', 'D'), ('D', 'E'), ('E', 'A'), ('E', 'B'), ('E', 'C'), ('E', 'D'), ('E', 'E')]
✅ 중복조합 combinations_with_replacement
중복을 허용한 조합
from itertools import combinations_with_replacement
# for i in combinations_with_replacement(반복가능한 객체 , 뽑을숫자):
for i in combinations_with_replacement([1,2,3,4], 2):
print(i, end=" ")
# >>> (1, 1) (1, 2) (1, 3) (1, 4) (2, 2) (2, 3) (2, 4) (3, 3) (3, 4) (4, 4)
참조
(Python) 순열, 조합, 중복순열, 중복조합 쉽게 구현하기
(Python) 순열, 조합 쉽게 만들기¶결론부터 말하자면, 라이브러리에서 불러온 함수와 직접 구현한 함수가 속도차이 10배정도를 보였다. (라이브러리가 훨씬 빠름) 파이썬 documentation에서 어떻게 구
juhee-maeng.tistory.com
'python' 카테고리의 다른 글
| Python의 print()안에 sep, end 파라미터 (0) | 2023.08.13 |
|---|---|
| Python의 Class 문법 ( feat. 객체지향 프로그래밍 , __init__ , self ) (0) | 2023.08.07 |
