| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- cta button
- 원시자료형
- 객체지향
- css
- OOP
- codestates
- 자바스크립트
- css in js
- Router
- WAI-ARIA
- 회고
- self reliance
- 프로토타입
- Javascript #코드스테이츠
- cta버튼
- 참조자료형
- codestate
- Prototype
- condestates
- frontend
- 프론트엔드
- 계산기
- html
- 코드스테이스
- 코드스테이츠
- 개발자
- JS
- CDD
- JavaScript
- 호스트인식
- Today
- Total
jh.nrtv
[자료구조] 재귀 (Recursion) , Tree , 트리순회 (BFS , DFS) 본문
✅ 재귀의 정의
재귀는 그래프 탐색, 트리, dp 등 주요 자료구조와 알고리즘에 접목된다.
재귀는 자신을 정의할 때, 자기 자신을 재호출 하는 것을 의미한다.
재귀의 구성요소
recurrence relation : 점화식
base case : 더이상 재귀호출을 하지 않아도 되는 상황(조건)
def factorial(n):
if n == 1: # base case
return 1
return n * factorial(n - 1) # 점화식재귀의 시간복잡도
재귀함수 전체의 시간복잡도 = 재귀함수 호출 수 x (재귀함수 하나당)시간복잡도
def factorial(n):
if n == 1:
return 1
return n * factorial(n - 1)
재귀 함수 호출 수
⇒ n
재귀 함수 하나 당 시간복잡도
⇒ O(1)
재귀의 시간 복잡도
⇒ O(n * 1)
def fibo(n):
if n == 1 or n == 2:
return 1
return fibo(n - 1) + fibo(n - 2)
재귀 함수 호출 수
⇒ 2^n
재귀 함수 하나 당 시간복잡도
⇒ O(1)
재귀의 시간 복잡도
⇒ O(2^n * 1)
✅ Tree
Tree의 정의
Tree는 서로 연결된 Node의 계층형 자료구조로써, root 와 부모-자식 관계의 subtree로 구성되어 있다.
리스트가 단순히 순서를 매겨 데이터를 나열 하는 선형 자료구조였다면, 트리는 비선형적인 자료구조이다.
트리 관련 개념
- 정점 (Vertex): A,B,C와 같은 값을 갖고 나타내며, 노드로 표현됩니다.
- 간선 (Edge): 정점 간에 연결된 선입니다.
- 자식 노드 (Child), 부모 노드 (Parent)
- 형제 노드(Sibling): 같은 부모를 가진 노드를 말합니다.
- 리프 노드 (Leef): 더 이상 뻗어나갈 수 없는 마지막 노드를 일컫습니다.
- 차수 (degree): 각 노드가 갖는 자식의 수. 모든 노드의 차수가 n개 이하인 트리를 n진 트리라고 합니다.
- 조상 (ancestor) 위쪽으로 간선을 따라가면 만나는 노드들 말합니다.
- 자손 (descendant): 아래쪽으로 간선을 따라가면 만나는 노드들을 말합니다.
- 루트 노드(Root): 트리의 시작 점 입니다. ( 맨 위 노드 )
- 높이 (height): 루트 노드에서 가장 멀리 있는 리프 노드 까지의 거리입니다. 즉, 리프 노드중에 최대 level 값
- 레벨 (level): 루트 노드에서 떨어진 거리입니다. ( root node= LV 0 )
- 서브트리 (subtree): 트리의 어떤 노드를 루트로 하고, 그 자손으로 구성된 트리를 subtree라고 한다.
이진 트리 Binary Tree
모든 노드의 차수가 2 이하인 트리 ( 3진트리, 4진트리도 존재함)
완전 이진 트리 Complete Binary Tree
상위 노드부터 차수를 두 개씩 가득 채운 2진트리
✅ 트리 순회 Tree Traversal
트리 순회란 트리 탐색이라고 불리우며 각 노드를 방문(!= 접근)하는 과정을 말한다. 순회 방법으로는 너비 우선 탐색 (BFS)와 깊이 우선 탐색 (DFS)가 있다.
- '접근'과 '방문'은 다르다. 접근은 여러 번 할 수 있으나, 방문은 한 번씩만 하는 코드를 구현하고자 한다.

🔸 BFS Breadth-First Search ( 너비 우선 탐색 )
시작노드와 가까운 노드부터 먼 노드 순으로 방문하는 방법 Level Order Traversal (= level에 따라서 순차적으로 방문하는 방법 )
Queue 활용해서 구현
아래의 코드의 대략적 구현방향은 다음과 같다.
1. 왼쪽 그림과 같이 루트에서 가까운 노드를 순서대로 방문해야 한다. 현 노드들의 자식노드들은 즉시 방문처리(visited)를 한다.
2. 또한 1에 연결된 3,4 가 2에 연결된 5,6보다 먼저 방문해야 하기에 '1번의 자식노드를 먼저 방문하고 , 2번의 자식으로 가세요' 라는 순서를 기록해야 한다.
3. 그 순서를 q 라는 queue 자료구조의 형태에 저장하고, 선입선출 구조로 각자 자식노드를 탐색한다.
4. q를 선입선출하며 q가 없어질 때까지, 즉 자식노드를 검사를 하지 않은 노드가 없을 때까지 반복한다.
graph = {
0: [1, 3, 6],
1: [0, 3],
2: [3],
3: [0, 1, 2, 7],
4: [5],
5: [4, 6, 7],
6: [0, 5],
7: [3, 5],
}
start_v = 0
from collections import deque
def bfs(graph, start_v):
q = deque() #queue형태로 '자식노드 검사 대기줄'을 기록할 예정임
q.append(start_v) #시작노드 먼저 queue에
visited = {start_v: True} #현재 노드는 방문처리
while q:
cur_v = q.popleft()
for next_v in graph[cur_v]: #현 노드의 자식노드들 순회
if next_v not in visited: #만약 자식노드가 방문 이전이면
visited[next_v] = True #방문처리 해주고
q.append(next_v) #자식노드 검사 대기줄에 기록
print(bfs(graph, start_v))
# 0 ,1 ,3, 6, 2, 7, 5, 4
🔸 DFS Depth-First Seach ( 깊이 우선 탐색 )
재귀 활용해서 DFS 구현
- root 만 주면 모든 노드에 '접근' 하는 코드
def dfs( cur_node ) :
# 넘겨받은 node의 값이 None이면 return으로 순회를 멈춘다.
if cur_node is None :
return
# 각 노드의 left, right 노드를 재귀로 dfs에 넘겨주는데,
dfs( cur_node.left )
dfs( cur_node.right )
dfs(root)
def dfs(cur_v):
visited[cur_v] = True #현재 노드는 방문기록
for next_v in graph[cur_v]: #그래프에서 현재 노드에 연결되 자식노드 순회하는데
if next_v not in visited: #만약 자식노드가 방문 안되어있으면
dfs(next_v) #재귀 ->하면 현 노드 방문처리...자식노드 방문확인..현 노드 방문처리..
visited = {}
graph = {...}
dfs(0)🔸 DFS의 방문 종류 : 전위순회, 중위순회 , 후위순회
방문하다(visit) != 순회하다(traversal)
비슷하지만 약간의 뉘앙스가 다름. 트리에서의 순회 = "트리를 돌아 다니는 것" / 방문 = "노드의 값을 접근하는 것(출력, 저장 등의 행위)"
* 전위순회 , 중위순회, 후위순회 모두 DFS와 같은형태로 순회하지만 '방문'을 다르게 하는것!!
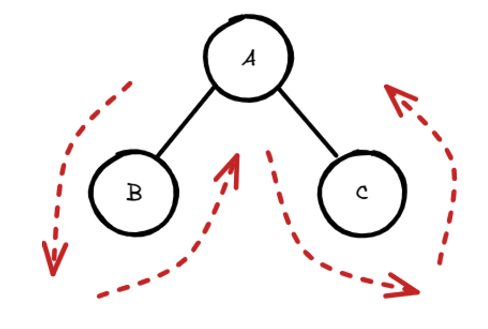
1. 전위순회 (preorder) - Root를 가장 먼저 방문
- 출력 순서: A(root), B(left), C(right)
- 나를 먼저 방문하고 자식 노드들을 방문한다.
def preorder(root):
if root is None:
return
print(root) #방문
preorder(root.left)
preorder(root.right)2. 중위순회 (inorder) - Root를 중간에 방문
- 출력 순서: B(left), A(root), C(right)
- 왼쪽 노드를 먼저 방문하고, 나를 방문한 후, 오른쪽 노드를 방문한다.
def inorder(root):
if root is None:
return
inorder(root.left) #left 먼저 보고
print(root) #루트 방문 후
inorder(root.right) #right 방문3. 후위순회 (postorder) - Root를 마지막에 방문
- 출력 순서: B(left), C(right), A(root)
- 자식노드들을 다 방문한 후, 나를 방문한다.
def postorder(root):
if root is None:
return
postorder(root.left) # 좌 , 우 모두 방문 후
postorder(root.right)
print(root) #루트 방문

전위순회 : A→B→C→D→E→F→G
중위순회 : C→B →D→A→F→E→G
후위순회 : C→D→B→F→G→E→A
추가 참조
07-01. 배열로 이진트리 표현하기
파이썬으로 이진트리를 표현 방법에 (1) 배열을 이용하는 것과 (2) 연결 리스트를 이용하는 것이 있다. 먼저 배열로 이진트리를 나타내보자. 아래 트리의 값을 레벨 순서대로 배…
wikidocs.net
BFS 참고영상
https://www.youtube.com/watch?v=CJiF-muKz30&t=345s
'알고리즘, 자료구조' 카테고리의 다른 글
| [알고리즘] JavaScript로 조합, 중복조합, 순열, 중복순열 구현하기 (0) | 2024.01.06 |
|---|---|
| [자료구조] 해시 테이블이란? (0) | 2023.12.16 |
| [자료구조] Python의 자료구조 - list, tuple, set, dictionary( =Hash Table) (0) | 2023.09.09 |
| [자료구조] Queue & Stack - Python으로 구현하기 (0) | 2023.09.08 |
| [자료구조] Linked List- Python으로 구현하기 (0) | 2023.08.13 |

